Hồi quy tuyến tính trong Python là gì ?
Hồi quy tuyến tính (Linear Regression) là một kỹ thuật học máy (machine learning) cơ bản được sử dụng để dự đoán giá trị của một biến phụ thuộc (dependent variable) dựa trên một hoặc nhiều biến độc lập (independent variables).
- Hồi Quy Tuyến Tính là gì ?
- Hồi quy tuyến tính với Python và scikit-learn
- Ứng dụng thực tế
- Video thực hành sử dụng hồi quy tuyến tính
Hồi quy tuyến tính tìm ra một hàm số tuyến tính, trong đó mối quan hệ giữa các biến được mô tả bằng một đường thẳng.
1. Hồi Quy Tuyến Tính là gì ?
Công thức hồi quy tuyến tính
Công thức chung của hồi quy tuyến tính đơn giản với một biến độc lập là:
Trong đó:
- là biến phụ thuộc (output),
- là biến độc lập (input),
- là hằng số (intercept),
- là hệ số (coefficient),
- là sai số (error).

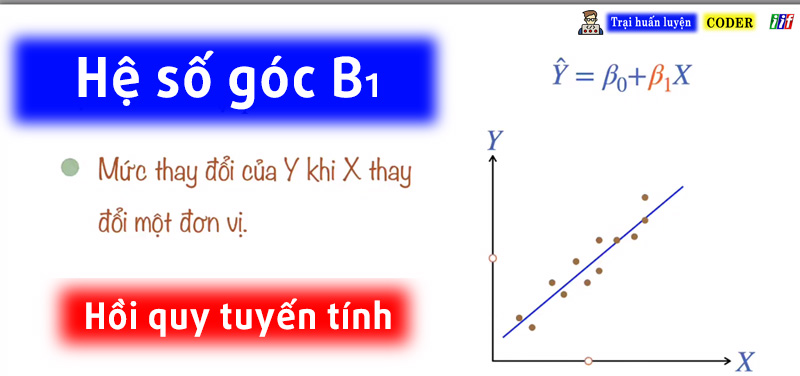
Hệ số góc
Ứng dụng hàm hồi quy tuyến tính trong lập trình nhất là python rất hiệu quả sử dụng để thống kê, dự đoán kết quả.
Bài toán dễ hiểu nhất về hồi quy tuyến tính
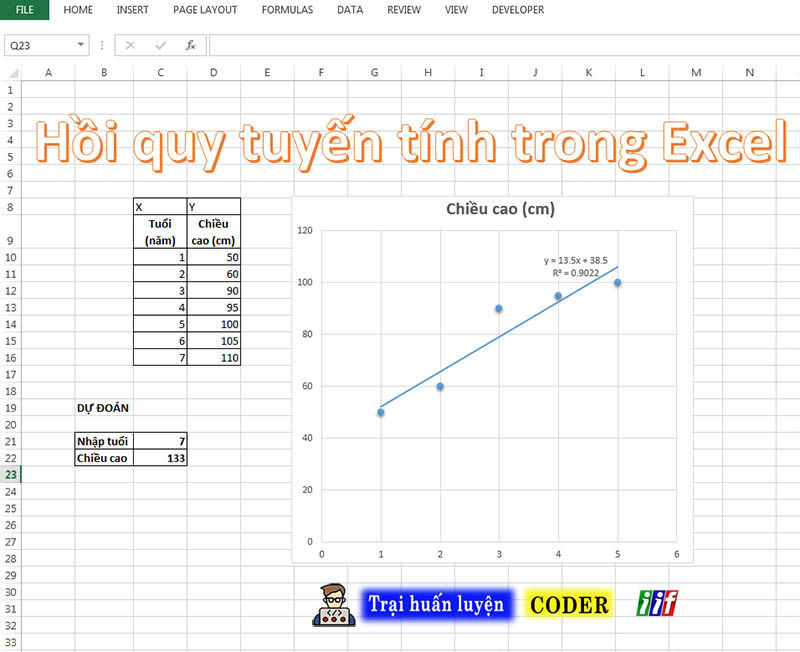
Dự đoán chiều cao dựa trên tuổi của trẻ em
Giả sử bạn là bác sĩ nhi khoa và bạn muốn dự đoán chiều cao của trẻ em dựa vào độ tuổi. Bạn biết rằng, theo kinh nghiệm, chiều cao của trẻ em có xu hướng tăng dần theo độ tuổi, nhưng không phải là một cách ngẫu nhiên mà có một mối quan hệ gần như tuyến tính (đi lên dần dần theo độ tuổi).
Mô tả tình huống
Bạn có dữ liệu các trẻ em đến khám bênh sổ tuổi và chiều cao như sau:
| Tuổi (năm) | Chiều cao (cm) |
|---|---|
| 3 | 90 |
| 4 | 95 |
| 5 | 100 |
| 6 | 105 |
| 7 | 110 |
Dữ liệu này cho thấy rằng, chiều cao có mối quan hệ trực tiếp với tuổi, và có thể vẽ ra một đường thẳng gần như đi qua tất cả các điểm dữ liệu.
Khi có liên quan thì tính hồi quy tuyến tính mới khả năng ứng dụng.
Câu hỏi: vậy trẻ em 8,9,10 tuổi chiều cao như thế nào ? cách dự đoán ? (cách code python)
Sử dụng hồi quy tuyến tính để dự đoán chiều cao trẻ em
Hồi quy tuyến tính giúp bạn tìm ra một đường thẳng mà bạn có thể sử dụng để dự đoán chiều cao của một đứa trẻ bất kỳ khi biết tuổi của chúng.
- X là biến độc lập, trong trường hợp này là tuổi của trẻ em.
- Y là biến phụ thuộc, trong trường hợp này là chiều cao của trẻ em.
- Mô hình hồi quy tuyến tính sẽ tìm ra một đường thẳng có dạng:
Trong đó:
- là chiều cao dự đoán (cm),
- là tuổi (năm),
- là độ dốc của đường thẳng (tỷ lệ thay đổi giữa tuổi và chiều cao),
- là điểm giao của đường thẳng với trục y (chiều cao khi tuổi là 0, có thể là điểm tham chiếu).
Kết quả:
Giả sử sau khi tính toán, bạn có được một công thức hồi quy tuyến tính:
Ý nghĩa của công thức:
- 5 là hệ số góc m, có nghĩa là mỗi năm tuổi, chiều cao sẽ tăng thêm 5 cm.
- 75 là hằng số , có thể hiểu là chiều cao của trẻ em khi mới sinh (tuổi 0), tuy nhiên, trong thực tế, chiều cao của trẻ sơ sinh thường khác, và số liệu này chỉ mang tính chất lý thuyết.
Dự đoán chiều cao:
Giờ bạn có thể dự đoán chiều cao của một đứa trẻ dựa trên độ tuổi của nó.
Ví dụ:
- Nếu bạn muốn biết chiều cao của một đứa trẻ 8 tuổi, bạn thay vào công thức:
Vậy, đứa trẻ 8 tuổi này dự đoán sẽ có chiều cao khoảng 115 cm.
Tóm lại: trên chỉ là giả thuyết, thực tế thì còn nhiều biến để ra kết quả.
2. Hồi quy tuyến tính với Python và scikit-learn
Scikit-lear là gì ?
scikit-learn (hay còn gọi là sklearn) là một thư viện học máy (machine learning) mã nguồn mở được viết bằng Python. Nó cung cấp các công cụ và thuật toán để xây dựng, huấn luyện và đánh giá các mô hình học máy. scikit-learn được thiết kế dễ sử dụng và phù hợp với các tác vụ như phân loại, hồi quy, phân cụm, giảm chiều dữ liệu, và đánh giá mô hình.
Các tính năng chính của scikit-learn
Các thuật toán học máy: scikit-learn cung cấp một loạt các thuật toán học máy như:
Hồi quy tuyến tính (Linear Regression)
Phân loại (Classification) như K-Nearest Neighbors, Logistic Regression, Support Vector Machines (SVM), v.v.
Phân cụm (Clustering) như K-Means, DBSCAN.
Giảm chiều dữ liệu (Dimensionality reduction) như PCA (Principal Component Analysis).
Ví dụ đơn giản về hồi quy tuyến tính với thư viện scikit-learn trong Python
Cài đặt thư viện scikit-learn
Trước tiên, bạn cần cài đặt thư viện scikit-learn nếu chưa cài: pip install scikit-learn
Code ví dụ hồi quy tuyến tính đơn giản
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
# Dữ liệu: Tuổi và Chiều cao
X = np.array([1, 2, 3, 4, 5, 6, 7]).reshape(-1, 1) # Tuổi (một chiều)
y = np.array([50, 60, 90, 95, 100, 105, 110]) # Chiều cao (cm)
# Khởi tạo mô hình hồi quy tuyến tính
model = LinearRegression()
# Huấn luyện mô hình với dữ liệu
model.fit(X, y)
# Dự đoán chiều cao cho một số độ tuổi mới
new_ages = np.array([8, 9, 10]).reshape(-1, 1) # Các độ tuổi mới cần dự đoán
predicted_heights = model.predict(new_ages)
# In kết quả dự đoán
for age, height in zip(new_ages.flatten(), predicted_heights):
print(f"Dự đoán chiều cao cho trẻ {age} tuổi: {height:.2f} cm")
# Vẽ đồ thị thể hiện mối quan hệ giữa tuổi và chiều cao
plt.scatter(X, y, color='blue') # Dữ liệu gốc
plt.plot(X, model.predict(X), color='red') # Đường hồi quy
plt.xlabel("Tuổi (năm)")
plt.ylabel("Chiều cao (cm)")
plt.title("Hồi quy tuyến tính: Tuổi vs Chiều cao")
plt.show()Giải thích đoạn code python trên
- Dữ liệu:
Xlà độ tuổi của trẻ em vàylà chiều cao tương ứng. Vì scikit-learn yêu cầu mảng hai chiều cho các đặc trưng (features), nên chúng ta phải chuyển đổiXthành mảng 2 chiều vớireshape(-1, 1). - Mô hình hồi quy tuyến tính: Chúng ta sử dụng
LinearRegression()để tạo một mô hình hồi quy tuyến tính. - Huấn luyện mô hình: Sử dụng
fit(X, y)để huấn luyện mô hình với dữ liệu. - Dự đoán chiều cao: Sau khi huấn luyện, mô hình có thể dự đoán chiều cao cho các độ tuổi mới (8, 9, 10).
- Vẽ đồ thị: Để trực quan hóa, chúng ta vẽ đồ thị với các điểm dữ liệu gốc (diện tích và giá nhà) và đường hồi quy (được mô hình tạo ra).
Kết quả khi thực thi code
Khi chạy chương trình, bạn sẽ nhận được kết quả dự đoán chiều cao của trẻ ở độ tuổi 8, 9 và 10, cùng với đồ thị minh họa.
Dự đoán chiều cao cho trẻ 8 tuổi: 115.00 cm
Dự đoán chiều cao cho trẻ 9 tuổi: 120.00 cm
Dự đoán chiều cao cho trẻ 10 tuổi: 125.00 cm
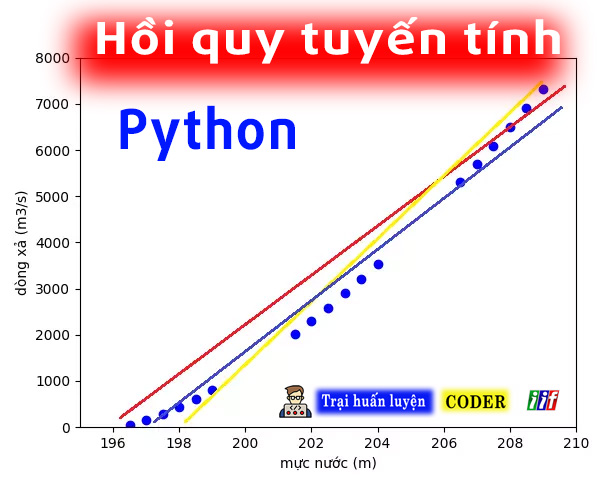
[Dự đoán giá thịt heo với hồi quy tuyến tính Python]
3. Ứng dụng thực tế
Hồi quy tuyến tính có thể được áp dụng trong rất nhiều bài toán thực tế như:
- Dự đoán giá nhà dựa trên diện tích.
- Dự đoán doanh thu dựa trên chi phí quảng cáo.
- Dự đoán tốc độ của một phương tiện dựa trên thời gian di chuyển.
4. Video thực hành sử dụng hồi quy tuyến tính
đang cập nhật...
Tìm kiếm:
- Cài và code Python trong vòng 10 phút
- Tài liệu Python (PDF) miễn phí
- Phần mềm lập trình python mà coder nên dùng
- Cú pháp Python
- Comment trong Python
- Cách in ra màn hình python
- Một số ký tự đặc biệt trong Python
- Làm việc với chuỗi trong Python
- Hàm print trong python
- Nguyên lý cấp phát bộ nhớ cho biến trong Python
- Biến và kiểu dữ liệu trong Python
- Ép kiểu dữ liệu trong Python
- Kiểu ngày trong Python
- Hàm input trong python
- Mệnh đề so sánh trong Python
- Biểu thức trong Python
- Câu lệnh if trong Python
- Vòng lặp Python
- Một số hàm toán học trong python
- Các hàm xử lý chuỗi trong Python
- Hàm trong Python
- Phân biệt hai kiểu hàm trong python để hiểu bản chất
- Mảng trong Python
- Dictionary trong Python
- Quản lý file và thư mục trong Python
- Lập trình hướng đối tượng trong Python
- Quản lý lỗi trong Python
- Trí tuệ nhân tạo với Python
- Lập trình Web với Python
- Hồi quy tuyến tính trong Python là gì ?
- Số thực và số nguyên trong Python
- Sai lệch số thực trong Python
- Khi nào dùng from datetime import datetime , khi nào import datetime trong python
- So sánh del và pop() trong biển kiểu danh sách Python
- Tạo ứng dụng nhận diện khuôn mặt bằng Python
- Tạo ứng dụng Chatbot bằng Python
- Tuples và Sets trong Python
- Mẹo học Python hiệu quả
- Xử lý ngoại lệ (Exception Handling) trong Python
- Khóa học Python miễn phí
- MicroPython là gì ?
- Cấu hình IIS với python
- Pseudocode - Thuật toán mã giả trong Python
Hồi quy tuyến tính (Linear Regression) là một kỹ thuật học máy (machine learning) cơ bản được sử dụng để dự đoán giá trị của một biến phụ thuộc (dependent variable) dựa trên một hoặc nhiều biến độc lập (independent variables).